Golang program for implementation of AVL Trees

package main
 
import (
    "encoding/json"
    "fmt"
)

type Key interface {
    Less(Key) bool
    Eq(Key) bool
}
 

type Node struct {
    Data    Key
    Balance int
    Link    [2]*Node
}
 

func opp(dir int) int {
    return 1 - dir
}
 
// single rotation
func single(root *Node, dir int) *Node {
    save := root.Link[opp(dir)]
    root.Link[opp(dir)] = save.Link[dir]
    save.Link[dir] = root
    return save
}
 
// double rotation
func double(root *Node, dir int) *Node {
    save := root.Link[opp(dir)].Link[dir]
 
    root.Link[opp(dir)].Link[dir] = save.Link[opp(dir)]
    save.Link[opp(dir)] = root.Link[opp(dir)]
    root.Link[opp(dir)] = save
 
    save = root.Link[opp(dir)]
    root.Link[opp(dir)] = save.Link[dir]
    save.Link[dir] = root
    return save
}
 
// adjust valance factors after double rotation
func adjustBalance(root *Node, dir, bal int) {
    n := root.Link[dir]
    nn := n.Link[opp(dir)]
    switch nn.Balance {
    case 0:
        root.Balance = 0
        n.Balance = 0
    case bal:
        root.Balance = -bal
        n.Balance = 0
    default:
        root.Balance = 0
        n.Balance = bal
    }
    nn.Balance = 0
}
 
func insertBalance(root *Node, dir int) *Node {
    n := root.Link[dir]
    bal := 2*dir - 1
    if n.Balance == bal {
        root.Balance = 0
        n.Balance = 0
        return single(root, opp(dir))
    }
    adjustBalance(root, dir, bal)
    return double(root, opp(dir))
}
 
func insertR(root *Node, data Key) (*Node, bool) {
    if root == nil {
        return &Node{Data: data}, false
    }
    dir := 0
    if root.Data.Less(data) {
        dir = 1
    }
    var done bool
    root.Link[dir], done = insertR(root.Link[dir], data)
    if done {
        return root, true
    }
    root.Balance += 2*dir - 1
    switch root.Balance {
    case 0:
        return root, true
    case 1, -1:
        return root, false
    }
    return insertBalance(root, dir), true
}
 
// Insert a node into the AVL tree.
func Insert(tree **Node, data Key) {
    *tree, _ = insertR(*tree, data)
}

// Remove a single item from an AVL tree.
func Remove(tree **Node, data Key) {
    *tree, _ = removeR(*tree, data)
}

func removeBalance(root *Node, dir int) (*Node, bool) {
    n := root.Link[opp(dir)]
    bal := 2*dir - 1
    switch n.Balance {
    case -bal:
        root.Balance = 0
        n.Balance = 0
        return single(root, dir), false
    case bal:
        adjustBalance(root, opp(dir), -bal)
        return double(root, dir), false
    }
    root.Balance = -bal
    n.Balance = bal
    return single(root, dir), true
}
 
func removeR(root *Node, data Key) (*Node, bool) {
    if root == nil {
        return nil, false
    }
    if root.Data.Eq(data) {
        switch {
        case root.Link[0] == nil:
            return root.Link[1], false
        case root.Link[1] == nil:
            return root.Link[0], false
        }
        heir := root.Link[0]
        for heir.Link[1] != nil {
            heir = heir.Link[1]
        }
        root.Data = heir.Data
        data = heir.Data
    }
    dir := 0
    if root.Data.Less(data) {
        dir = 1
    }
    var done bool
    root.Link[dir], done = removeR(root.Link[dir], data)
    if done {
        return root, true
    }
    root.Balance += 1 - 2*dir
    switch root.Balance {
    case 1, -1:
        return root, true
    case 0:
        return root, false
    }
    return removeBalance(root, dir)
}
 

type intKey int 
func (k intKey) Less(k2 Key) bool { return k < k2.(intKey) }
func (k intKey) Eq(k2 Key) bool   { return k == k2.(intKey) }
 
func main() {
    var tree *Node
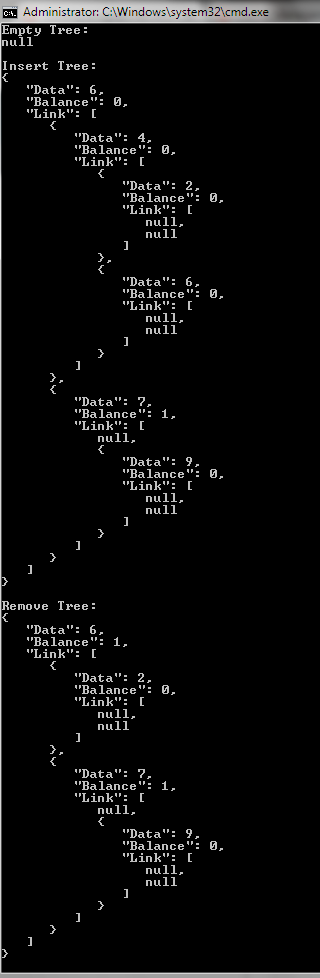
    fmt.Println("Empty Tree:")    
	avl,_ := json.MarshalIndent(tree, "", "   ")
	fmt.Println(string(avl))

    fmt.Println("\nInsert Tree:")
    Insert(&tree, intKey(4))
    Insert(&tree, intKey(2))
    Insert(&tree, intKey(7))
    Insert(&tree, intKey(6))
	Insert(&tree, intKey(6))
    Insert(&tree, intKey(9))
    avl,_ = json.MarshalIndent(tree, "", "   ")
	fmt.Println(string(avl))
 
    fmt.Println("\nRemove Tree:")
    Remove(&tree, intKey(4))
    Remove(&tree, intKey(6))
    avl,_ = json.MarshalIndent(tree, "", "   ")
	fmt.Println(string(avl))
}